Separating Axis Theorem
The Separating Axis Theorem (SAT) provides a way to find the intersection between any n-sided convex polygon or circle. In this tutorial, I will explain how this theorem works, and how you can use it to both detect and resolve collisions in your simulation.
Explanation of Separating Axis Theorem
SAT makes use of vector projection to figure out whether or not two concave polygons are intersecting. I believe the best way to describe it is to show you the instance where two polygons do not intersect.
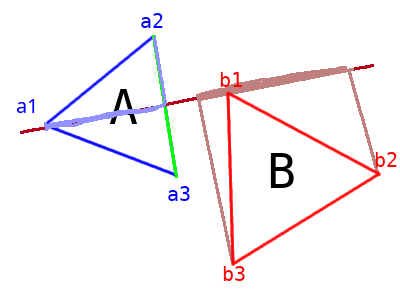
Images two shapes A and B as shown below (they are triangles here, but they can be anything really).
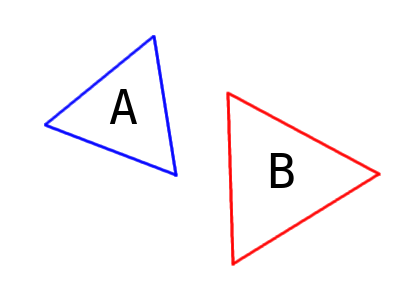
We know inutitively that if we were able to draw a line between the two objects, that means that they're not intersecting. In this case, that line is a vertical-ish line:
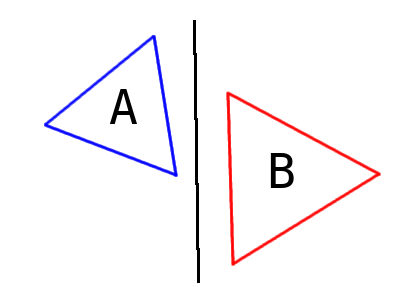
That line could be any of the infinite number of lines between the objects, so we can't really select that exact line. So the problem becomes: how do we infer that the vertical line shown in the previous diagram is a line that splits the objects? That is where the Separating Axis Theorem comes in.
To do separating axis theorem, we iterate all of the edges of both shapes. For each edge, we get the normal at that edge (In two-dimensions, this amounts to getting the perpendicular of the line segment defined by the two points of the edge).
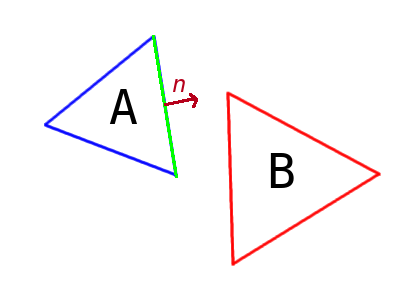
We then, in our heads, extend this normal to create an axis across our scene (keep in mind that you won't have to do any "extending" of this axis in code; the normal will do just fine).
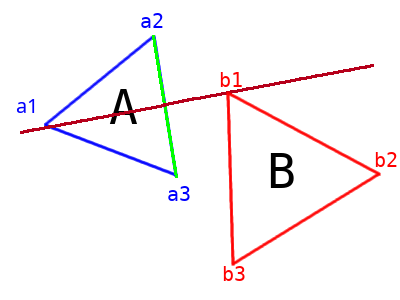
At this point, you will see that I named the three vertices on each of the triangles. Triangle A is made of vertices a1, a2, a3 and triangle B is made of vertices b1, b2, b3. At this point, we project the shape onto the axis. To do this, we project the vertices of each shape onto the axis to figure out which one maximizes the dot product and which one minimizes the dot product. The projection of the shape is then the range defined by this min and max value.
Finally, we check if the two ranges overlap. If they don't overlap, then the shapes do not intersect. If they do overlap, we repeat the process for all of the other edges. If all of these ranges overlap, then the shape overlaps, and there is no separating line between them.

Algorithm for Finding the Intersection
Given two polygons A and B:
- For each edge on A, get the normal n of that edge.
- Project each vertex v of A onto n. Return the minimum and maximum projection of all vertices as the projection of the shape.
- Repeat Step 2 for polygon B.
- If the min and max projections found in Steps 2 and 3 do NOT overlap, the polygons are not intersecting. Return false.
- If the projections overlap for each edge of both shapes, the shapes are intersecting. Return true.
Vector2 getProjection(Vector2* vertices, int numVertices, Vector2 axis) {
// Find the min and max vertex projections
float32 min = axis.dot(vertices[0]);
float32 max = min;
for (int v = 1; v < numVertices; v++) {
float32 d = axis.dot(vertices[v]);
if (d < min) {
min = d;
} else if (d > max) {
max = d;
}
}
return Vector2 { min, max };
}
bool projectionsOverlap(Vector2 first, Vector2 second) {
return first.x <= second.y && second.x <= first.y;
}
bool doIntersect(ConvexPolygon* first, ConvexPolygon* second) {
IntersectionResult ir;
// Check agaisnt the edges of the first polygon
for (int i = 0; i < first->numVertices; i++) {
Vector2 normal = first->edges[i].normal;
Vector2 firstProj = getProjection(first->transformedVertices, first->numVertices, normal);
Vector2 secondProj = getProjection(second->transformedVertices, second->numVertices, normal);
if (!projectionsOverlap(firstProj, secondProj)) {
return false;
}
}
// Check against the edges of the second polygon
for (int i = 0; i < second->numVertices; i++) {
Vector2 normal = second->edges[i].normal;
Vector2 firstProj = getProjection(first->transformedVertices, first->numVertices, normal);
Vector2 secondProj = getProjection(second->transformedVertices, second->numVertices, normal);
if (!projectionsOverlap(firstProj, secondProj)) {
return false;
}
}
return true;
}
SAT Collision Resolution
Now that we know that our objects have intersected, we want to send them tumbling away from one another in order to simulate a collision. To do this, we will need to find the following things:
- Point of Application: at what point on each object did the objects first intersect
- Collision Normal: in what direction, point towards object A, did the polygons intersect
- Relative Velocity: easily found by taking the difference between the two velocities.
Finding the Intersecting Edge
We can already figure out that the following two triangles intersect one another:
We know that A can only intersect B if: (1) a vertex from A is inside of B, (2) an edge of A flatly intersects an edge of B, or (3) a vertex of A overlaps exactly a vertex of B. Honestly, for our purposes, scenarios 2 and 3 are quite unlikely, but we can explore them a bit just to see how we might resolve them. We will start with the first case, since it is more likely. We will start by drawing the axis defined by the leftmost edge of B with both polygons projected onto it:
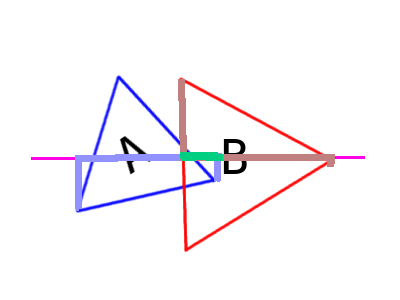
This is a poorly drawn picture, but you should be able to see that the bit in green represents the intersection between the projections of the two polygons. If we were to repeat this same exercise for every edge here, we'll begin to see something very interesting. And, if we take new shapes and continue this stategy, we can begin to come to a very elegant conclusion:
The intersecting edge will be the one where the projection of triangle A overlaps with the projection of triangle B the least!
I'm sure someone more inclined to proving mathematical truities would love to describe this to you, but, for all intents and purposes, this intutitive understanding is good enough for us. We just want to make games, anyhow.