Physics for Games

Separating Axis Theorem

The Separating Axis Theorem (SAT) provides a way to find the intersection between any n-sided convex polygon or circle. In this tutorial, I will explain how this theorem works, and how you can use it to both detect and resolve collisions in your simulation.

Explanation of Separating Axis Theorem

SAT makes use of vector projection to figure out whether or not two concave polygons are intersecting. I believe the best way to describe it is to show you the instance where two polygons do not intersect.

Images two shapes A and B as shown below (they are triangles here, but they can be anything really).


We know inutitively that if we were able to draw a line between the two objects, that means that they're not intersecting. In this case, that line is a vertical-ish line:


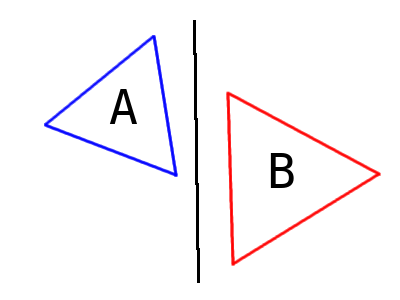
That line could be any of the infinite number of lines between the objects, so we can't really select that exact line. So the problem becomes: how do we infer that the vertical line shown in the previous diagram is a line that splits the objects? That is where the Separating Axis Theorem comes in.

To do separating axis theorem, we iterate all of the edges of both shapes. For each edge, we get the normal at that edge (In two-dimensions, this amounts to getting the perpendicular of the line segment defined by the two points of the edge).


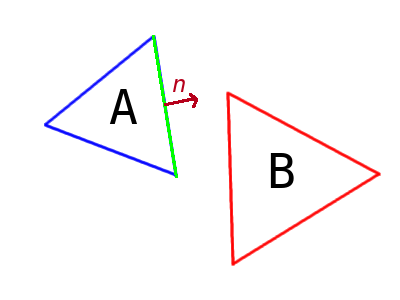
We then, in our heads, extend this normal to create an axis across our scene (keep in mind that you won't have to do any "extending" of this axis in code; the normal will do just fine).

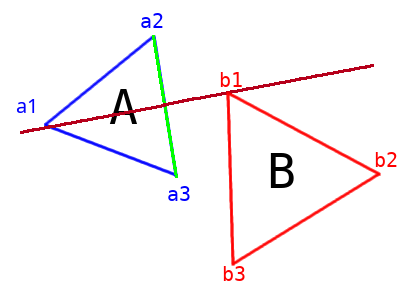
At this point, you will see that I named the three vertices on each of the triangles. Triangle A is made of vertices a1, a2, a3 and triangle B is made of vertices b1, b2, b3. At this point, we project the shape onto the axis. To do this, we project the vertices of each shape onto the axis to figure out which one maximizes the dot product and which one minimizes the dot product. The projection of the shape is then the range defined by this min and max value.


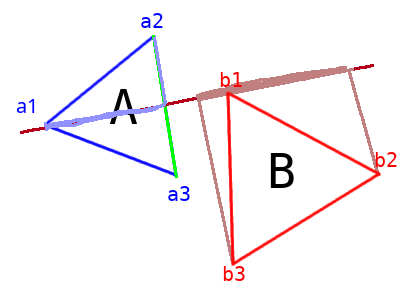
Finally, we check if the two ranges overlap. If they don't overlap, then the shapes do not intersect. If they do overlap, we repeat the process for all of the other edges. If all of these ranges overlap, then the shape overlaps, and there is no separating line between them.


Algorithm for Finding the Intersection

Given two polygons A and B:

  1. For each edge on A, get the normal n of that edge.
  2. Project each vertex v of A onto n. Return the minimum and maximum projection of all vertices as the projection of the shape.
  3. Repeat Step 2 for polygon B.
  4. If the min and max projections found in Steps 2 and 3 do NOT overlap, the polygons are not intersecting. Return false.
  5. If the projections overlap for each edge of both shapes, the shapes are intersecting. Return true.
And that is all there is to finding the intersection between two convex polygons. Here is the code snippet that does this if you are interested: 
Vector2 getProjection(Vector2* vertices, int numVertices, Vector2 axis) {
    // Find the min and max vertex projections
    float32 min = axis.dot(vertices[0]);
    float32 max = min;

    for (int v = 1; v < numVertices; v++) {
        float32 d = axis.dot(vertices[v]);

        if (d < min) {
            min = d;
        } else if (d > max) {
            max = d;
        }
    }

    return Vector2 { min, max };
}

bool projectionsOverlap(Vector2 first, Vector2 second) {
    return first.x <= second.y && second.x <= first.y;
}

bool doIntersect(ConvexPolygon* first, ConvexPolygon* second) {
    IntersectionResult ir;

    // Check agaisnt the edges of the first polygon
    for (int i = 0; i < first->numVertices; i++) {
        Vector2 normal = first->edges[i].normal;

        Vector2 firstProj = getProjection(first->transformedVertices, first->numVertices, normal);
        Vector2 secondProj = getProjection(second->transformedVertices, second->numVertices, normal);

        if (!projectionsOverlap(firstProj, secondProj)) {
            return false;
        }
    }

    // Check against the edges of the second polygon
    for (int i = 0; i < second->numVertices; i++) {
        Vector2 normal = second->edges[i].normal;

        Vector2 firstProj = getProjection(first->transformedVertices, first->numVertices, normal);
        Vector2 secondProj = getProjection(second->transformedVertices, second->numVertices, normal);

        if (!projectionsOverlap(firstProj, secondProj)) {
            return false;
        }
    }

    return true;
}

SAT Collision Resolution

Now that we know that our objects have intersected, we want to send them tumbling away from one another in order to simulate a collision. To do this, we will need to find the following things:

  • Point of Application: at what point on each object did the objects first intersect
  • Collision Normal: in what direction, point towards object A, did the polygons intersect
  • Relative Velocity: easily found by taking the difference between the two velocities.

Finding the Intersecting Edge

We can already figure out that the following two triangles intersect one another:



We know that A can only intersect B if: (1) a vertex from A is inside of B, (2) an edge of A flatly intersects an edge of B, or (3) a vertex of A overlaps exactly a vertex of B. For our purposes, scenario 3 is quite unlikely, so we can ignore it for now. We will start with the first case, since it is the most likely.

The following drawing shows both of our objects projected onto the axis defined by object B's leftmost edge:



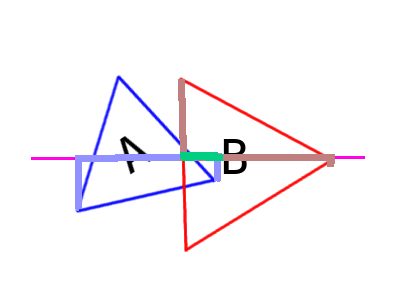
If you were to repeat this exercise of projecting the shapes onto every axis of both shapes, you will begin to unconver an interesting truth: The intersecting edge will be the one where the projection of triangle A overlaps with the projection of triangle B the least! This should be unsurprising if you consider it. If our simulation is running quickly enough, the point of object A that is penetrating the edge of object B will just barely be inside of B. At the same time, it should be the only point that is currently inside of B. Hence, the overlap of the projection on that axis will be from that edge of B to that point on A. Knowing that this edge caused the intersection, we now have the collision normal.

Finding which point causes the intersection

This part is made easy by the fact that we know which edge of object B caused the intersection in the first place. We know, then, that the intersecting point on object A must be the point that is currently inside of B. Simply put, this point will be the vertex of A that was projected onto that axis that is closest to the edge of B. This will be true so long as the simulation is properly fast and the object is not infinitesmley small (in which case, we're dealing with particle physics, and you shouldn't be using this tutorial).

Algorithm for Collision Resolution

Given two polygons A and B:

  1. Find the intersecton as before
  2. While finding the intersection, keep track of the axis that the projection on object A overlapped with the corresponding projection on object B the least. Remember the edge that this that held this axis.
  3. Using this axis, find out which point on the other object inside of the edge by comparing the distances from the two points on the edge to the two points projected onto the axis created by that edge.
  4. Use the calcualted edge to find the normal and the overlap point to find the point of application.
And that is it! Here is the code for this algorithm: 
struct IntersectionResult {
    bool intersect = false;
    Vector2 collisionNormal;
    Vector2 relativeVelocity;
    Vector2 firstPointOfApplication;
    Vector2 secondPointOfApplication;
};

struct Edge {
    Vector2 normal;
    Vector2 start;
    Vector2 end;
};

struct SATResult {
    Edge* minOverlapEdge = NULL;        // Edge that caused the intersection (on the 'first' shape)
    Vector2 overlapPoint;               // Point that caused the intersection (on the 'second' shape)
    float32 minOverlap = FLT_MAX;       // Smallest projection overlap
};

struct ProjectionResult {
    Vector2 minVertex;
    Vector2 maxVertex;
    Vector2 projection;
};

// Given the vertices in the shape, we find the min and max vertices that project
// onto the axis. We also save which vertices were which so that we can resolve
// the collision later.
ProjectionResult getProjection(Vector2* vertices, int numVertices, Vector2 axis) {
    ProjectionResult pr;
    pr.minVertex = vertices[0];
    pr.maxVertex = vertices[0];
    float32 min = axis.dot(vertices[0]);
    float32 max = min;

    for (int v = 1; v < numVertices; v++) {
        float32 d = axis.dot(vertices[v]);

        if (d < min) {
            pr.minVertex = vertices[v];
            min = d;
        } else if (d > max) {
            pr.maxVertex = vertices[v];
            max = d;
        }
    }
    
    pr.projection = Vector2 { min, max };
    return pr;
}

bool projectionsOverlap(Vector2 first, Vector2 second) {
    return first.x <= second.y && second.x <= first.y;
}

float32 getProjectionOverlap(Vector2 first, Vector2 second) {
    float32 e = MIN(first.y, second.y);
    float32 f = MAX(first.x, second.x);
    return e - f;
}

bool runSatForShapesEdges(SATResult* result, ConvexPolygon* first, ConvexPolygon* second) {
    for (int i = 0; i < first->numVertices; i++) {
        Vector2 normal = first->edges[i].normal;

        ProjectionResult firstProj = getProjection(first->transformedVertices, first->numVertices, normal);
        ProjectionResult secondProj = getProjection(second->transformedVertices, second->numVertices, normal);

        if (!projectionsOverlap(firstProj.projection, secondProj.projection)) {
            return false;
        }

        float32 overlap = getProjectionOverlap(firstProj.projection, secondProj.projection);
        if (overlap < result->minOverlap) {
            result->minOverlap = overlap;
            result->minOverlapEdge = &first->edges[i];
            
            // The overlapPoint will be the point on the other shape that penetrated the edge.
            // If we caught the intersection reasonably early, it should be the point on 'second'
            // that is nearest to the points on 'first'.
            float32 min1min2 = (firstProj.minVertex - secondProj.minVertex).length();
            float32 min1max2 = (firstProj.minVertex - secondProj.maxVertex).length();
            float32 max1max2 = (firstProj.maxVertex - secondProj.maxVertex).length();
            float32 max1min2 = (firstProj.maxVertex - secondProj.minVertex).length();
            
            float32 closest = MIN(min1min2, MIN(min1max2, MIN(max1max2, max1min2)));
            if (closest == min1min2 || closest == max1min2) {
                result->overlapPoint = secondProj.minVertex;
            } else {
                result->overlapPoint = secondProj.maxVertex;
            }
        }
    }

    return true;
}

const float32 EPSILON = 1.f;
IntersectionResult getIntersection(ConvexPolygon* first, ConvexPolygon* second) {
    IntersectionResult ir;
    SATResult sat;
    
    if (!runSatForShapesEdges(&sat, first, second)) {
        return ir;
    }

    if (!runSatForShapesEdges(&sat, second, first)) {
        return ir;
    }

    ir.intersect = true;
    ir.relativeVelocity = first->body.velocity - second->body.velocity;
    ir.collisionNormal = sat.minOverlapEdge->normal;
    ir.firstPointOfApplication = sat.overlapPoint - first->body.position;
    ir.secondPointOfApplication = sat.overlapPoint - second->body.position;;

    return ir;
}

Live Example of Intersection Detection

A live example of Separating Axis Theorem running with full collision detection. Click to reverse gravity on the simualtion.